Riccardo Gonzo

Riccardo Gonzo

A theoretical physicist exploring the intersection of high-energy physics and general relativity, who fell in love with amplitudes and gravitational waves.

Research interests

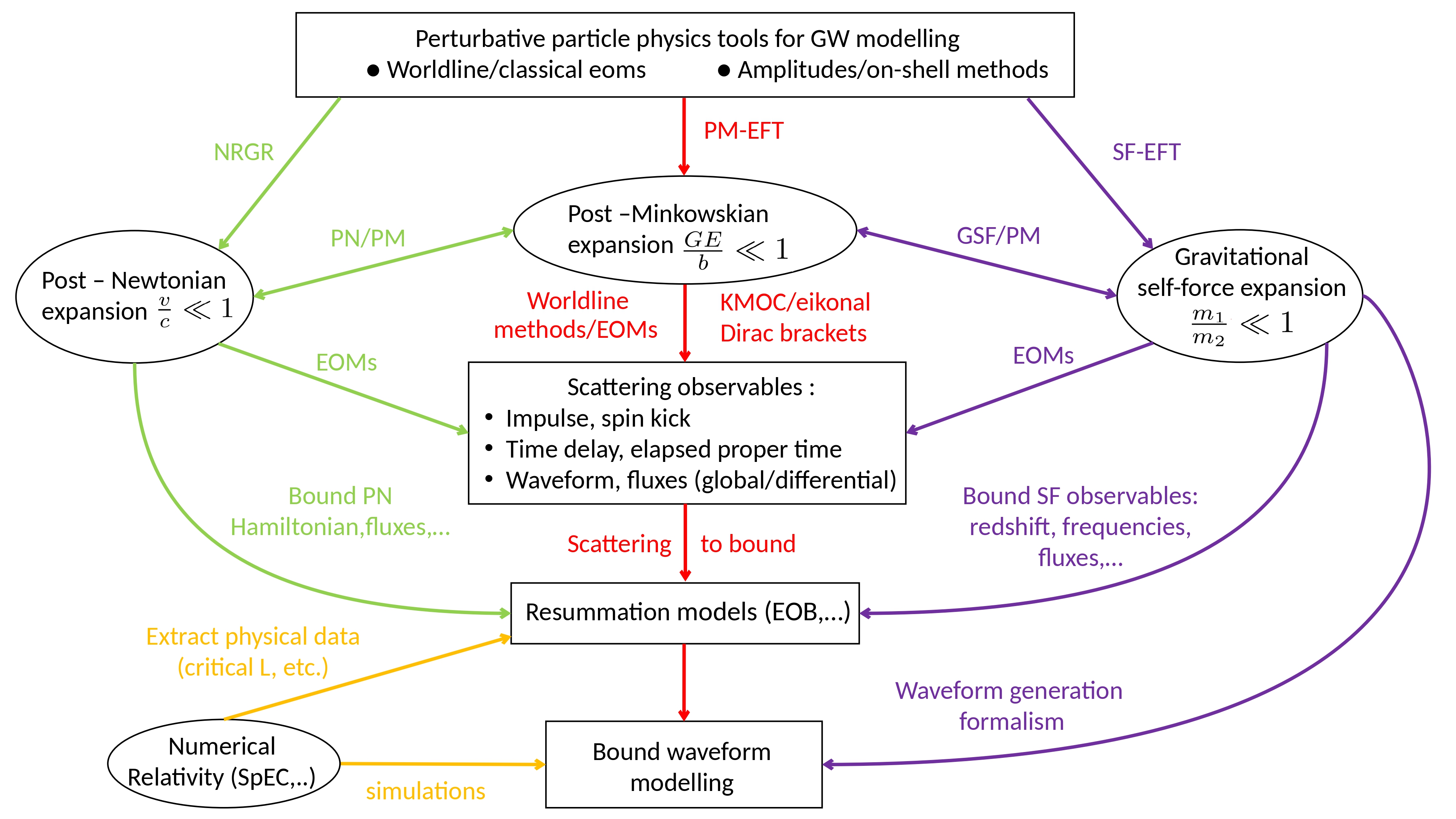
Research framework diagram

My Work at a Glance

I am a theoretical physicist interested in understanding the fundamental laws of nature, currently working at the intersection of high-energy physics and general relativity. My current work focuses on the analytical description of gravitational binary systems and the modelling of their waveforms by combining modern particle physics tools — such as scattering amplitudes — with traditional general relativity methods like the self-force expansion. My aim to create a unified framework that connects weak-field Post-Minkowskian and Post-Newtonian theory with strong-field methods from the self-force approach, leading to improved waveform models for current (LIGO–Virgo–KAGRA) and future (LISA) gravitational wave detectors. Looking ahead, my dream is to establish an international research group dedicated to advancing the synergy between scattering amplitudes and gravitational-wave science.

Gravitational Waveforms from Scattering Amplitudes

Together with A. Cristofoli, D. Kosower and D. O’Connell, I helped establish a framework to compute gravitational waveforms directly from on-shell scattering amplitudes in the post-Minkowskian expansion. With various collaborators, I also studied a novel extension of the eikonal formalism using coherent states, showing how classical gravitational waves emerge from the quantum point-particle description.

Most recently, with F. Alessio and C. Shi, I defined a new set of classical generating functionals from the S-matrix formalism. Within this setting, all two-body scattering observables can be derived in gauge-invariant form through the application of Dirac brackets, providing an efficient framework for the analytic modeling of precessing Kerr black hole binaries.

Scatter-to-Bound Dictionary for Kerr Geodesics and Waveforms

With C. Shi, I established novel gauge-invariant maps between scattering and bound geodesic observables in Kerr spacetime, formulating the analytic continuation between scattering and bound actions and related observables for generic orbits.

With T. Adamo and A. Ilderton, I developed a classical Bethe–Salpeter framework that connects the analytic S-matrix to the bound dynamics, showing how scattering waveforms can be resummed into periodic bound-state waveforms. This construction shows that a resummation of the weak-field expansion is essential to recover orbital periodicity. The gravitational self-force framework naturally implements this resummation, providing a bridge between perturbative scattering data and bound-state dynamics. Along this line, I co-authored with J. Lewis and A. Pound the "first law of black-hole scattering", relating elapsed proper time directly to the Detweiler redshift — a central gauge-invariant building block for waveform modeling.

Self-Force EFT for Kerr BHs: Resummation from Weak to Strong-field

With D. Akpinar and V. del Duca, I constructed the first spinning self-force EFT at first self-force order (1SF), deriving the related effective action for Kerr black holes to quadratic order in spin and reformulating the equation for the metric perturbation in this framework.

This framework revealed new spinning recoil operators and established a direct relation between weak-field post-Minkowskian expansions and strong-field self-force results. It further highlights promising resummation strategies for extending the weak-field expansion into the strong-field regime, especially near the separatrix between scattering and plunging orbits where point-particle divergences emerge.

Research Highlights

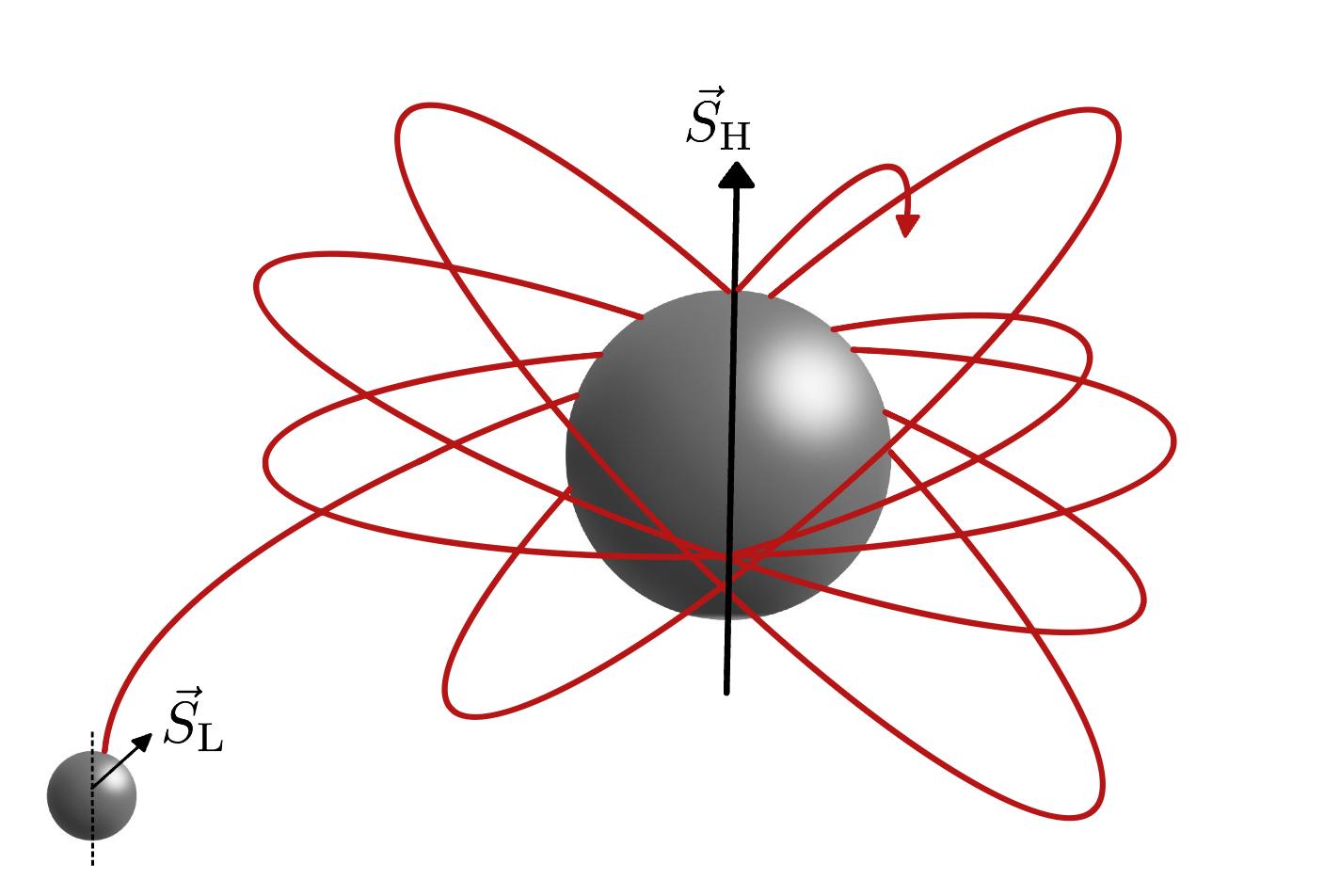
Publication 1

The spinning self-force EFT: 1SF waveform recursion relation and Compton scattering

Dogan Akpinar, Vittorio Del Duca, Riccardo Gonzo — Phys. Rev. D 112, 084014 (2025)

Development of an effective-field-theory framework at first self-force order for spinning binaries; with a new waveform recursion relation and novel connections between weak and strong-field.

Publication 2

Scattering and bound observables for spinning particles in Kerr spacetime with generic spin orientations

Riccardo Gonzo, Canxin Shi — Physical Review Letters 133, 221401 (2024)

Novel on-shell Dirac bracket framework relating the radial action to observables for test spinning particles in Kerr, with interesting implications for the scatter-to-bound map for precessing spinning binaries.

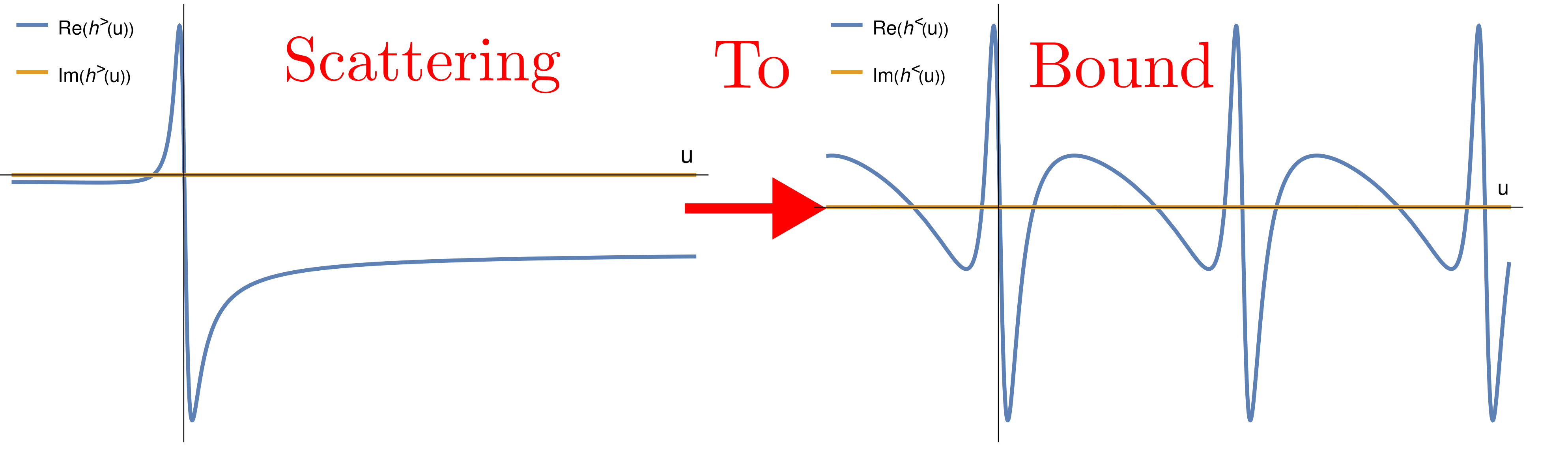
Publication 3

Gravitational bound waveforms from amplitudes

Tim Adamo, Riccardo Gonzo, Anton Ilderton — JHEP 05 (2024) 034

New scatter-to-bound map for the instantaneous contributions to the classical gravitational waveform from the S-matrix, suggesting a new on-shell route to GW modeling for black hole binaries.

News & Media Coverage

First Law of Binary Black Hole Scattering

The spinning self-force EFT: 1SF waveform recursion relation and Compton scattering

Waveforms from amplitudes

Media & popular-science coverage